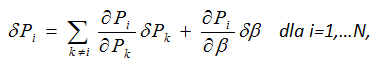Analiza strukturalna trendów (AST) stanowi modyfikację metody cross-impact analysis (CIA), która pozbawiona jest wad tej metody związanych z subiektywnością ocen prawdopodobieństw i brakami formalnymi modelu probabilistycznego metody CIA. AST jest również analizą wzajemnego wpływu trendów, jednak metoda analizy polega na traktowaniu trendów jako zdarzeń, polegających na zmianie wartości modelowanych zmiennych zgodnie z wyznaczonymi współczynnikami trendu, a następnie na zastosowaniu metody WAT do analizy tak otrzymanych zdarzeń. Interakcja przyszłych zdarzeń jest następnie modelowana jako sterowany system zdarzeń dyskretnych. W ten sposób metoda AST pozwala ocenić również wzajemne oddziaływania różnorodnych zmiennych, modelowanych jako trendy.
Pierwszym krokiem AST jest zdefiniowanie zdarzeń i trendów, które będą brane pod uwagę. Włączenie nieistotnych zmiennych skomplikuje całą analizę i może negatywnie wpłynąć na adekwatność otrzymanych wyników. AST jest uproszczona, jeśli zdarzenia są od siebie niezależne. Następnym krokiem jest oszacowanie początkowych prawdopodobieństw dla każdego zdarzenia, równoznacznych z prawdopodobieństwami wystąpienia tych zdarzeń w przyszłości w określonym horyzoncie prognostycznym. Wyboru trendów i zdarzeń oraz oszacowania ich prawdopodobieństw dokonują eksperci z danej dziedziny, można również skorzystać z większości danych uzyskanych w badaniu delfickim.
Początkowe prawdopodobieństwa oszacowywane są przy założeniu, że inne trendy i zdarzenia występują i są wzajemnie zależne. W tym przypadku AST może być użyta do modyfikacji początkowych prawdopodobieństw innych zdarzeń w podobny sposób, jak ma to miejsce w przypadku zdarzeń przyszłych. Zatem przy oszacowaniu prawdopodobieństw każdego zdarzenia możliwość zaistnienia pozostałych zdarzeń brana jest pod uwagę od początku analizy. W tym przypadku AST jest stosowana do określenia czy oceny (opinie ekspertów) dotyczące początkowych i warunkowych prawdopodobieństw są spójne. Wykorzystując AST można również określić, jak wystąpienie nowego nieoczekiwanego zdarzenia (nie uwzględnionego w zdefiniowanym zbiorze N zdarzeń) wpłynie na prawdopodobieństwa wystąpienia wszystkich zdefiniowanych zdarzeń.
Jeżeli przy oszacowaniu prawdopodobieństwa zdarzenia Zi uwzględnia się możliwość wystąpienia pozostałych zdarzeń, to prawdopodobieństwo Pi można wyrazić jak funkcję prawdopodobieństw zdarzeń pozostałych:
|
|
(1) |
Powyższa funkcja może również zawierać dodatkowe zmienne wyrażające wpływ zdarzeń niezdefiniowanych pierwotnie w zbiorze zdarzeń początkowych.
W kolejnym kroku oszacowujemy prawdopodobieństwa warunkowe dla każdej kombinacji różnych trendów i zdarzeń. Są one zdefiniowane jako „nowe prawdopodobieństwo zdarzenia A pod warunkiem wystąpienia zdarzenia B”. Dla każdej pary zdarzeń lub trendów można przy tym uwzględnić ograniczenia na dopuszczalne wartości prawdopodobieństw warunkowych.
Jeżeli wystąpi zdarzenie Zk wpływające na prawdopodobieństwo wystąpienia zdarzenia Zi, to zmiana prawdopodobieństwa Pi opisana jest równaniem:
|
|
(2) |
gdzie: b jest miarą wpływu zdarzeń nieuwzględnionych w początkowym zbiorze N zdarzeń. Dla każdej pary zdarzeń A,B={Z1,…ZN},, prawdopodobieństwo początkowe zdarzenia A można przedstawić jako:
![]()
Zastępując najmniejszą wartość P(A/B’) przez 0 oraz największą wartość P(A/B’) przez 1 oraz korzystając z prawdopodobieństw początkowych, dla każdej kombinacji N zdefiniowanych zdarzeń początkowych otrzymamy ograniczenia na prawdopodobieństwa wystąpienia zdarzenia A pod warunkiem wystąpienia zdarzenia B:
|
|
(3) |
Następnie w oparciu o zależność (3) dokonywana jest kalibracja macierzy strukturalnej.
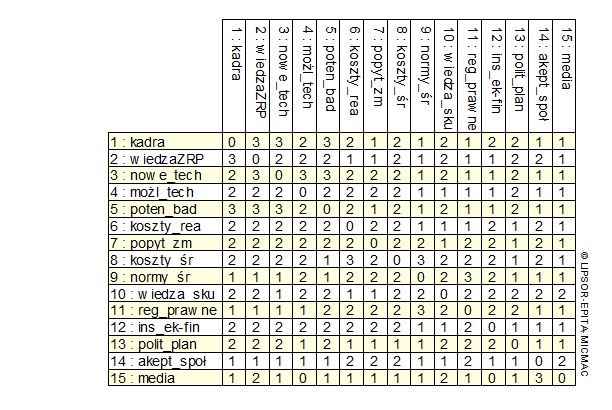
Rys. Przykład macierzy wpływów bezpośrednich.
Opracowanie: FPB